We have worked on statistical methodology development in the following projects, which were motivated by prominent biomedical research questions. The methods we developed have great potential to become critical tools in computational biology and medical informatics.

First, we have developed a “new R²” association measure for describing complex gene interactions. Capturing important gene expression relationships is a key component in computational biology research (e.g. network study). Commonly used measures such as Pearson correlation and Spearman rank correlation can only capture one-to-one relationships, but some transcription factors and their target genes may exhibit relationships such as a mixture of activation and repression. In [1], we proposed this new association measure as a generalization of the coefficient of determination R² to capture such relationships. This measure is based on a new non-parametric regression framework that is capable of describing sparse nonfunctional relationships between variables.

Second, in [2] we proposed a new procedure to construct confidence intervals for coefficients in high-dimensional linear models. Our procedure “BootstrapLPR” (BootstrapLasso + Partial Ridge) is based on a two-stage estimator: using Lasso to select features and subsequently using Partial Ridge to refit the coefficients. Extensive simulation results show that compared with the benchmark de-sparsified Lasso methods, BootstrapLPR has on average 35%-50% shorter confidence interval lengths and is more robust to model mis-specification. We provide theoretical guarantee of BootstrapLPR under appropriate conditions and implemented it in the R package “LPR.”

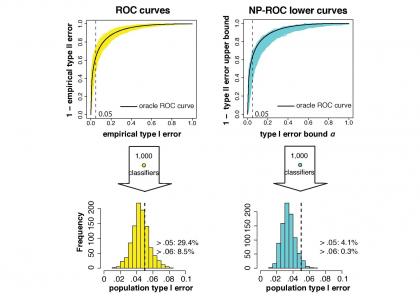
Third, in [3] we developed an umbrella algorithm for implementing binary classification methods under the Neyman-Pearson (NP) paradigm, as well as a new evaluation metric “NP-ROC” (Neyman-Pearson Receiver Operating Characteristics) band for evaluating NP classification methods. In many binary classification applications such as disease diagnosis and spam detection, practitioners often face great needs to control type I errors (e.g., chances of missing a malignant tumor) under some desired threshold. The NP classification paradigm is a theoretic framework to address such needs, as it aims to minimize population type II errors while installing some upper bound α on population type I errors. Our NP umbrella algorithm and NP-ROC band will serve as new effective tools to construct, evaluate, and compare binary classifiers aiming for population type I error control. Our work is currently funded by an NSF grant.

Fourth, in [4] we proposed a generative stochastic block model for bipartite networks with covariates. The motivation for this model is a prominent question in gene expression analysis: how do we simultaneously cluster genes in two species given both gene expression levels and the conservation relationships among genes? In the setting of our model, the conservation information is encoded in a bipartite network with genes as nodes and conservation relationships as edges, and gene expression levels are the node covariates. Our proposed inference method for the model is a generalization of the community detection methods for bipartite networks without node covariates.

References:

[1] Li. J.J., Tong, X., and Bickel, P.J. (2018). Generalized R2 measures for a mixture of bivariate linear dependences. Manuscript.

[2] Liu, H., Xu, X., and Li, J.J. (2018). A bootstrap lasso + partial ridge method to construct confidence intervals for parameters in high-dimensional sparse linear models. Statistica Sinica in press.

[3] Tong, X., Feng, Y., and Li, J.J. (2018). Neyman-Pearson (NP) classification algorithms and NP receiver operating characteristics (NP-ROC). Science Advances 4(2):eaao1659.

[3] Razaee, Z., Amini, A., and Li, J.J. (2018). Matched bipartite block model with covariates. Manuscript.